Among the most intriguing Mayan artifacts is the Dresden Codex, one of the few surviving Mayan books. The ancient Maya civilization, renowned for its sophisticated understanding of the cosmos, left behind a treasure trove of astronomical knowledge. Including within the codex which contains a detailed eclipse table. A recent study details how Mayan calendar specialists designed and refined this predictive tool. The study revises over a century of interpretations. It reveals how the table evolved from a general lunar calendar to a precise eclipse predictor. This article explores the key findings, historical context, and implications for our understanding of Mayan astronomy.
The Dresden Codex: A Window into Mayan Celestial Knowledge

The Dresden Codex is a pre-Columbian Mayan book dating back to around the 11th or 12th century CE. It’s currently housed in the Saxon State and University Library in Dresden, Germany. Written on bark paper with hieroglyphs and illustrations, it includes almanacs for tracking celestial events. This includes Venus cycles, lunar phases, and eclipses. The eclipse table, spanning pages 51-58, has long fascinated scholars for its apparent ability to forecast solar eclipses.
The study by researchers John Justeson and Justin Lowry builds on prior work by astronomers like Floyd Lounsbury. Lounsbury, in the 1970’s, proposed models for Mayan lunar calculations. However, the new study argues that the table’s 405-month length wasn’t originally for eclipses. Determining it was adapted from a broader lunar calendar. the authors analyzed historical eclipse data, mathematical models, and hieroglyphic texts. They reconstructed how Mayan “daykeepers” iteratively improved the table over centuries.
Key Findings: How the Eclipse Table Was Designed
The core of the paper lies in its explanation of the table’s structure and evolution.
Origins in a General Lunar Calendar
- 405-Month Framework: The table lists 69 new moon dates over 405 lunations (lunar months), with 55 intended as potential eclipse stations. Justeson and Lowry show this length was first used in a general lunar table, not specifically for eclipses. It commensurates lunar cycles with the 260-day “divinatory calendar” (tzolk’in), where intervals like 44 and 88 months align closely with multiples of 260 days minus one.
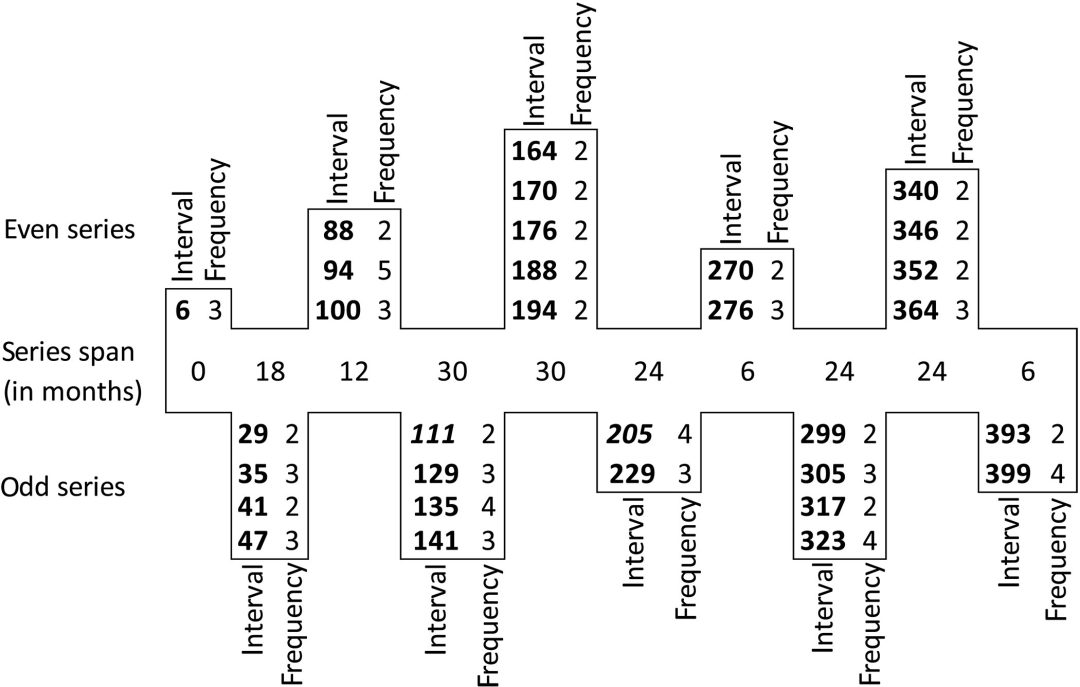
- Lunar Modeling: The authors endorse Lounsbury’s 1447:49 day-to-month ratio for calculating lunar intervals, derived from continued fractions approximating the average lunation (29.530589 days). This model fits 89% of 98-month spans in historical data from Monte Alban (ancient Zapotec site), suggesting Maya adapted similar ratios.
Eclipse Prediction Mechanism
- Stations and Intervals: Eclipse-possible dates occur in groups of six (or once seven) at 177-day intervals (about six lunations), separated by 11- or 17-month gaps due to the eclipse node’s 173.31-day cycle. The paper categorizes 55 stations as “real” (observable) and 14 as “contrived” (included for structural consistency but not eclipse-viable).
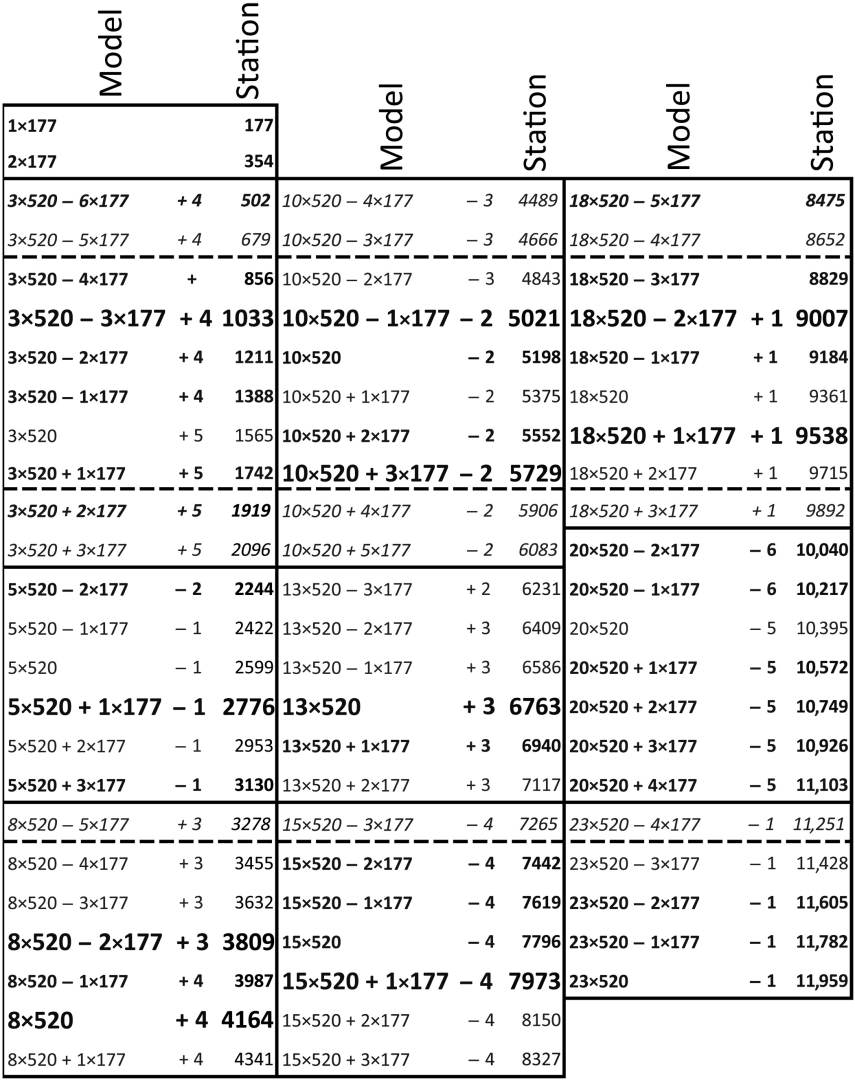
- Overlapping Tables: Contrary to prior assumptions that new tables started from the end of the previous one, the study proposes overlaps at 223 or 358 lunations to maintain accuracy. A mix of resets (four at 358 months for each at 223) yields a 1655-lunation cycle that predicts eclipses reliably for millennia.
Historical Reconstruction
- Observable Eclipses: Using data from 145 solar eclipses visible in Mayan lands (356-1148 CE), the authors identify frequent intervals like 669 months (triple saros) and 493/1162 months. These informed the table’s design, starting from Teotihuacan-influenced periods around 361 CE, when lunar counts first appear in Mayan texts.
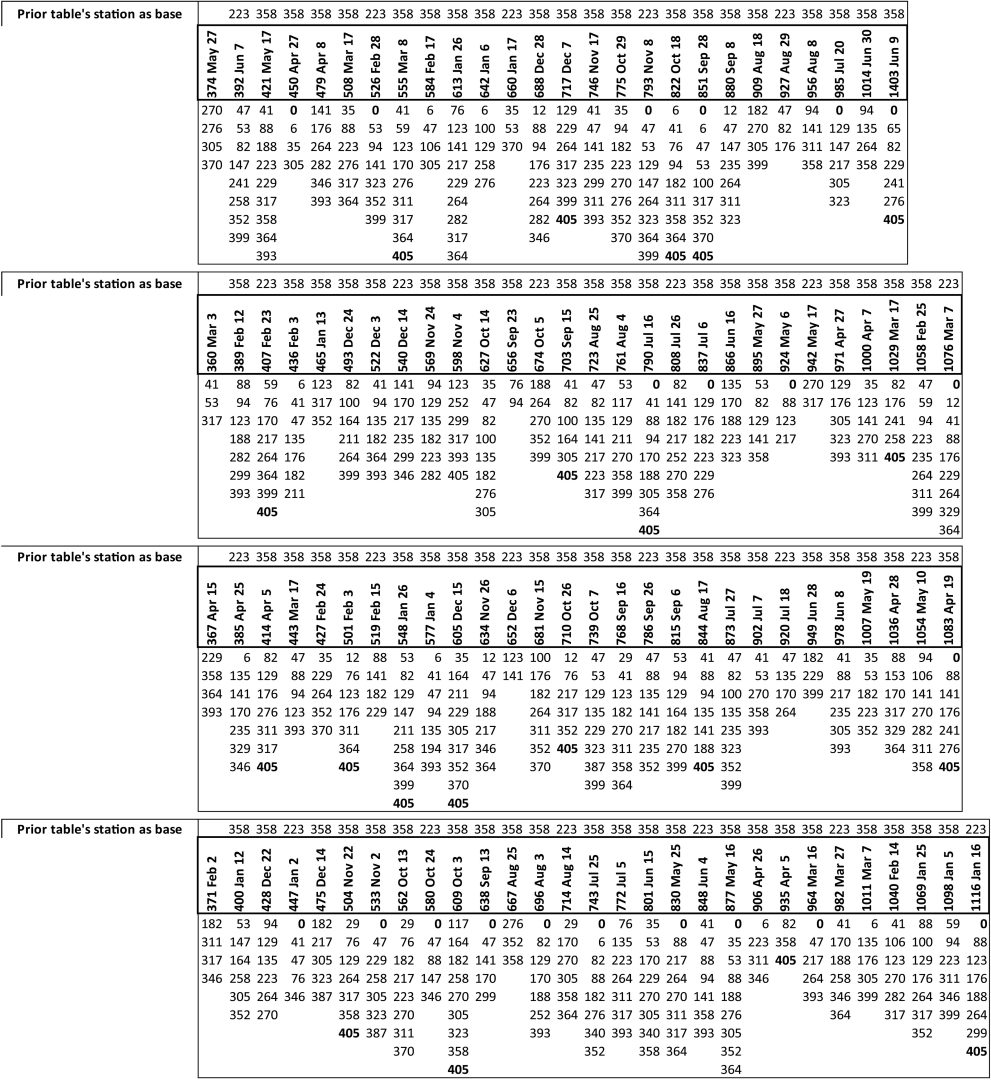
- Evolution Over Time: Early observations (e.g., 356-454 CE) showed repeating intervals like 94, 100, and 111 months, stimulating the eclipse model’s development. The paper outlines 21 possible historical sequences of tables, with 16 viable from pre-Classic eras.
Mathematical Underpinnings: Lunar and Eclipse Cycles Explained
For those interested in the technical side, the paper delves into Mayan computational models:
- Lunar Month Approximation: The 1447/49 ratio gives an average of 29.530612 days per lunation, accurate to within seconds over centuries.
- Abnodal Limits: Eclipses are possible within ±11.775 days of nodal passage in the Maya lowlands, refining Lounsbury’s broader range.
- Frequency Distributions: Intervals among historical eclipses (e.g., 176 months occurring 28 times) match the table’s stations, supporting a data-driven design.
These models highlight the Maya’s empirical approach, blending observation with calendar commensuration.
Implications for Mayan Astronomy and Modern Science
This research not only revises our view of the Dresden Codex but also underscores the Maya’s advanced predictive astronomy without telescopes. It suggests daykeepers used long-term records to refine tools, anticipating eclipses from ~500 BCE to the Post-Classic era.
This study offers evidence of iterative, observation-based science. Connecting broader topics like ancient calendars, celestial mechanics, and indigenous knowledge systems. Future studies could explore parallels with other Mesoamerican codices or integrate AI for eclipse simulations.
Conclusion: A Timeless Legacy of Celestial Mastery
This revelation transforms our understanding of the Mayan eclipse table, portraying it as a dynamic tool honed over generations. By linking it to lunar calendars and historical observations, the study reveals the ingenuity of Mayan daykeepers.
For More Ancient Eclipse tales check out Babylon’s Eclipse Omens of Doom

